お断り
今更ですが、お断りを。当ブログは私が統計学の勉強する中で、ノートやメモの様なものを公開しているもので、内容が正しいことを保証するものではありません。むしろ、私の思い違いは指摘頂きたいです。
共分散
偏差平方和は、平均との差の二乗を合計したもの。それをデータの個数で割ったものが分散。分散の平方根をとったものが標準偏差。データのばらつきを表します。
それに対して、二軸のデータの標準偏差みたいなものが相関係数。それぞれのデータについてX軸の平均との差掛けるY軸の平均との差を合計したものが共分散。二つの値が共感する度合い(相関関係)を示しています。
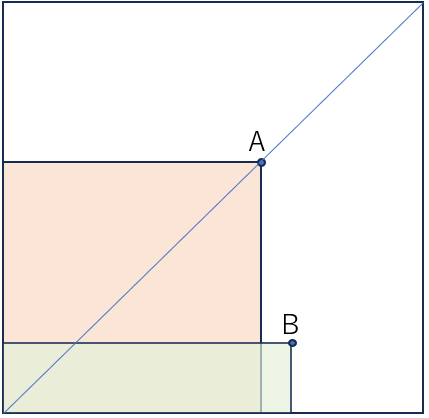
下の図のように、y=xの線上にある場合、一番相関関係が強い。点Aがつくる正方形の方が面積が大きいので点Bの作る長方形より面積が広い。つまり面積=二つの値が共感する度合いを示す、ということらしい。いったんこれはのみ込もう。
相関係数
共分散は、X軸の平均との差をY軸の平均との差を掛けているので、たとえば10ミリのものの共分散と1メートルのものの共分散は比較できない。そのため、共分散をXの標準偏差とYの標準偏差を掛けたもので割る。そうすると相関係数となり、使いやすくなります。
相関係数は、-1から+1の間の値をとり、0.7以上で強い相関があるといえるそうです。
0.7以上または-0.7以下: 強い相関がある
Perplexityより
0.4から0.7または-0.4から-0.7: 中程度の相関がある
0.2から0.4または-0.2から-0.4: 弱い相関がある
0.2未満または-0.2未満: ほとんど相関がない
数式を書く
折角なので、Latex形式で数式を書いてみることにします。調べながらで簡単ではありませんでしたが、それでもこの程度の手間で、数式が簡単に美しく描けるなんて、便利な時代になったものです。
これが相関係数の公式です。
\(
r_{xy}
= \frac{s_{xy}}{s_x s_y}
= \frac{\sum_{i = 1}^n (x_i - \bar{x})(y_i - \bar{y})}
{\sqrt{\sum_{i = 1}^n (x_i - \bar{x})^2}\sqrt{\sum_{i = 1}^n (y_i - \bar{y})^2}}
=\frac{1}{n}\sum_{i=1}^n \frac{x_i - \bar{x}}{s_x} \cdot \frac{y_i - \bar{y}}{s_y}
\)